股票买卖V

在原来几种的基础上多加了一个”冷冻期”的概念，即前一天卖出，今天就不能买入股票。

Acwing 和 Leetcode 本题题干一样，下面以 Acwing 为例。

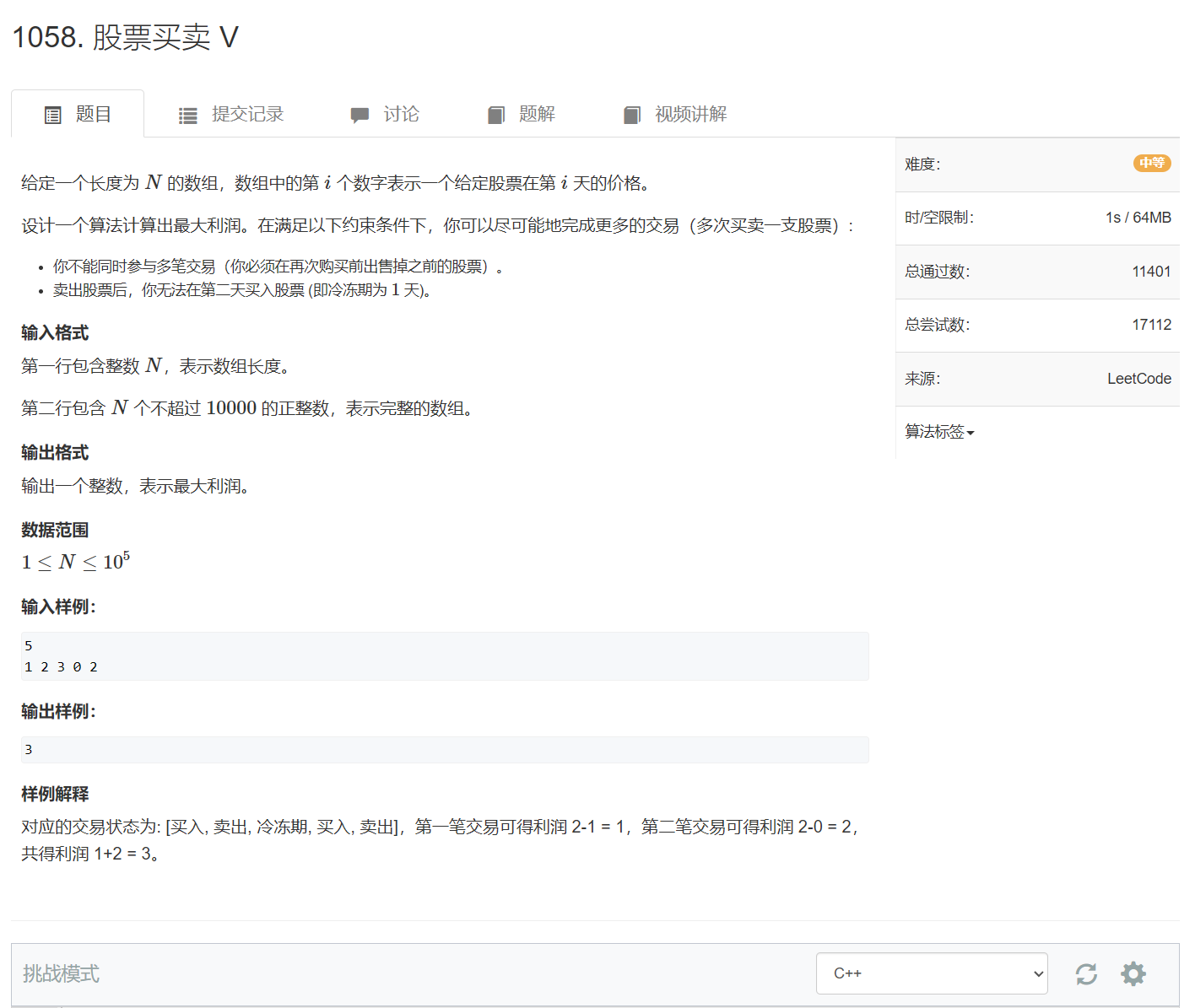
题目描述

题解

首先可以先回顾一下<[股票买卖 IV](买卖股票IV–状态机DP | KTnoobStation (gitee.io))>的状态表示, 本题还没限制交易笔数，所以还是有所区别的。

状态表示

根据题目要求，有冷藏期，则可将有货和无货两种状态进行进一步的划分。

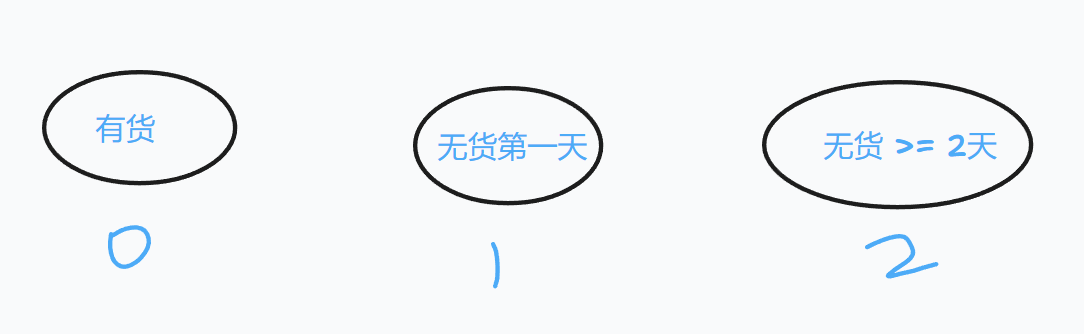
下面以上面的状态编号进行代指

其中 1 不能买入商品，2 可以买入商品。

状态转换

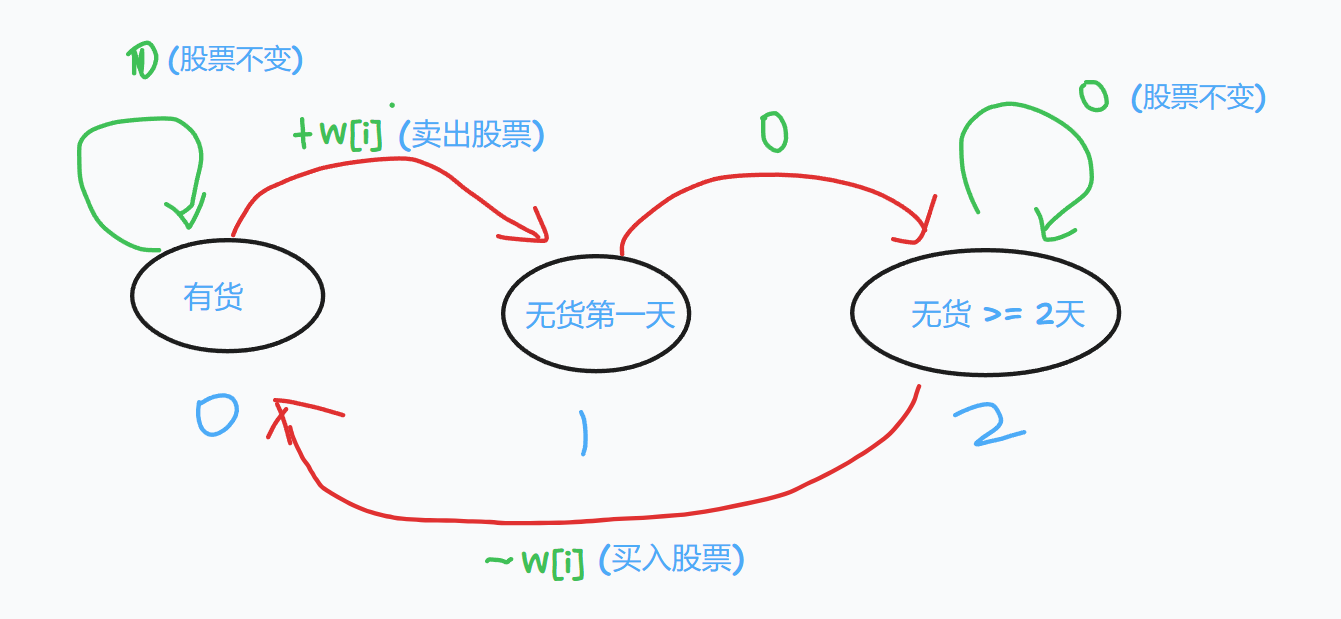
状态 0 ： 有货时，可以选择不卖，也可以选择卖出 + w[ i ]，则状态转为 1 ；
状态 1 ： 无货第一天，无法买入股票，自动转移到无货 >= 2 天的状态
状态 2 ： 无货第二天，可以买入，也可以不买，买的话则 - w[ i ] 到状态 0 ；

状态方程

现在只有状态表示和天数两个因素，则二维数组 f[N][M] 即可 N 为天数，M 为状态

N = 100010; M = 3;

注意出入口，哪条边能到达当前状态
状态 0 的方程： f[i][0] = max(f[i-1][0], f[i-1][2] - w[i]
状态 1 的方程： f[i][1] = f[i-1][0] + w[i]
状态 2 的方程： f[i][2] = max(f[i-1][2], f[i-1][1])
至此，方程写出来就好写代码了；

初始化的话：dp[0][0] = dp[0][1] = -INF; dp[0][2] = 0; 即第0 天不存在

代码实现

import java.util.*;
import java.io.*;

class Main{
    public static void main(String[] args) throws Exception{
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        
        int[] w = new int[n+1];
        int[][] dp = new int[n+1][3];
        
        for(int i = 1; i <= n; i++){
            w[i] = sc.nextInt();
        }
        
        dp[0][0] = dp[0][1] = -0x3f3f3f3f;
        dp[0][2] = 0;
        
        for(int i = 1; i <= n;i++){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][2] - w[i]);
            dp[i][1] = dp[i-1][0] + w[i];
            dp[i][2] = Math.max(dp[i-1][1], dp[i-1][2]);
        }
        System.out.println(Math.max(dp[n][1], dp[n][2]));  //最后一定是无货的
        
    }
}

附上 leetcode 上的解答:

class Solution {
    static final int INF = 0x3f3f3f3f;
    public int maxProfit(int[] prices) {
        int n = prices.length;

        if(n == 1) return 0;
        
        int[][] dp = new int[n+1][3];
        
        dp[0][0] = dp[0][1] = -INF;
        dp[0][2] = 0;
        
        for(int i = 1; i <= n;i++){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][2] - prices[i-1]);
            dp[i][1] = dp[i-1][0] + prices[i-1];
            dp[i][2] = Math.max(dp[i-1][1], dp[i-1][2]);
        }
        return Math.max(dp[n][1], dp[n][2]); //最后一定是无货的
    }
}