买卖股票IV--状态机DP

本文包括 ACWing 提高课一题以及力扣上的一题变式
Acwing: 1057. 股票买卖 IV - AcWing题库
Leetcode: 123. 买卖股票的最佳时机 III - 力扣（LeetCode）

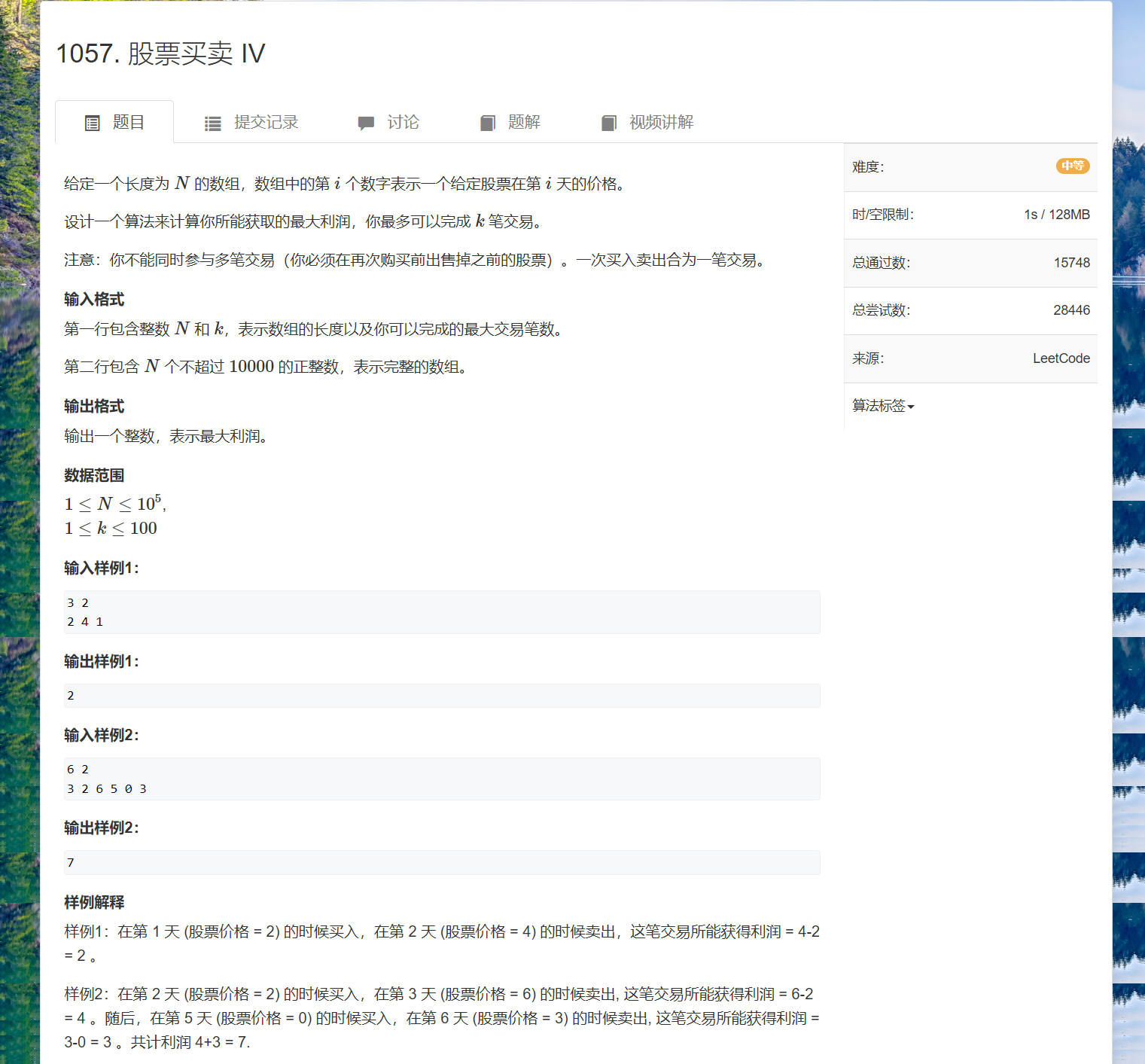
题目描述

解题思路

1. 划分当前持有股票状态有和无

2. 如果只是定义 DP 数组位 dp[i][j], 则只能说明前 i 天共有 j 次交易，区分不出状态

3. 因此多加一个属性，第 i 天在进行第 j 次交易时，当前是否持有股票，如 dp[i][j][0]; 无股票

4. 根据状态转换，dp[i][j][0] = max (dp[i-1][j][0], dp[i-1][j][1] + w[i]);
   解释：
   第 i 天如果没有持有股票，则由前一天状态过来后，j 次交易的最大利润和是”前一天没股票，
   则今天也无法获得收益（因为不持有股票）” 以及
   “前一天有股票，今天需要卖出股票才能达成 dp[i][j][0]的状态，因此是 dp[i-1][j][1] + w[i]” 中的最大值

• 同理： dp[i][j][1] ,如果前一天没股票，需要购买当前股票，则 dp[i-1][j-1][0] - w[i]; (买入算一次交易),有的话就不变，因为不能一天内同时进行多笔交易，则 dp[i-1][j][1]; 取 max
• 初始化，刚开始是无货的，j == 0 时，f[i][j][0] = 0 和 f[i][j][1] = -INF（因为没进行交易不可能有货）; 可以先将所有状态都初始化为 -INF, 然后再将 f[i][0][0]都更新为 0

最后因为空间问题，设置 dp 为 dp[2][N][M]; 但分析还是上述的

JAVA 版本

import java.util.*;
import java.io.*;


class Main{
    static int N = 100010, M = 110, INF = 0x3f3f3f3f;
    
    static int[][][] dp = new int [2][N][M];
    static int[] w = new int[N];
    
    public static void main(String[] args) throws IOException{
        Scanner scan = new Scanner(System.in);
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        
        String[] t = bf.readLine().split(" ");
        int n = Integer.parseInt(t[0]);
        int k = Integer.parseInt(t[1]);
        
        String[] str = bf.readLine().split(" ");
        
        for(int i = 1; i <= n;i++){
            w[i] = Integer.parseInt(str[i-1]);
        } 
        
        //初始化状态
        for (int i = 0; i < 2; i ++)
            for (int j = 0; j <= n; j ++)
                Arrays.fill(dp[i][j], -0x3f3f3f3f);
        
        for(int i = 0; i <= n;i++) dp[0][i][0] = 0;  //j为0，前 i 天 0 次交易，如果无货则为利润0;
        
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= k; j++){
                dp[0][i][j] = Math.max(dp[0][i-1][j], dp[1][i-1][j] + w[i]); //后面的是卖出
                dp[1][i][j] = Math.max(dp[1][i-1][j], dp[0][i-1][j-1] - w[i]); //后面的是买入,算一次交易
            }
        }
        int ans = 0;   //最多进行k次交易，不一定交易笔数越多，利润越高，枚举最大值
        for(int i = 0 ; i <= k; i++){
            ans = Math.max(dp[0][n][i], ans);
        }
        
        System.out.println(ans);
    }
}

力扣题目描述

C++版本

class Solution {

public:
    static const int N = 100010, M = 5;
    
    int maxProfit(vector<int>& prices) {
        int n = prices.size(); int k = 2;
        int dp[N][M][2];
        memset(dp,-0x3f, sizeof dp);

        //初始化0次交易0利润
        for(int i = 0; i <= n;i++){
            dp[i][0][0] = 0;
        }
        for(int i = 1;i <= n;i++){
            for(int j = 1; j <= k; j++){
                dp[i][j][0] = max(dp[i-1][j][1] + prices[i-1], dp[i-1][j][0]);
                dp[i][j][1] = max(dp[i-1][j-1][0] - prices[i-1], dp[i-1][j][1]);
            }
        }
        //最多两笔交易，但是可能不会发生交易，万一亏本呢
        int ans = 0;
        for(int i = 0; i <= k; i++){
            ans = max(ans, dp[n][i][0]);  //最后一定要是交易完成的结果
        }
        return ans;  
    }
};