拓扑排序

拓扑序列

定义

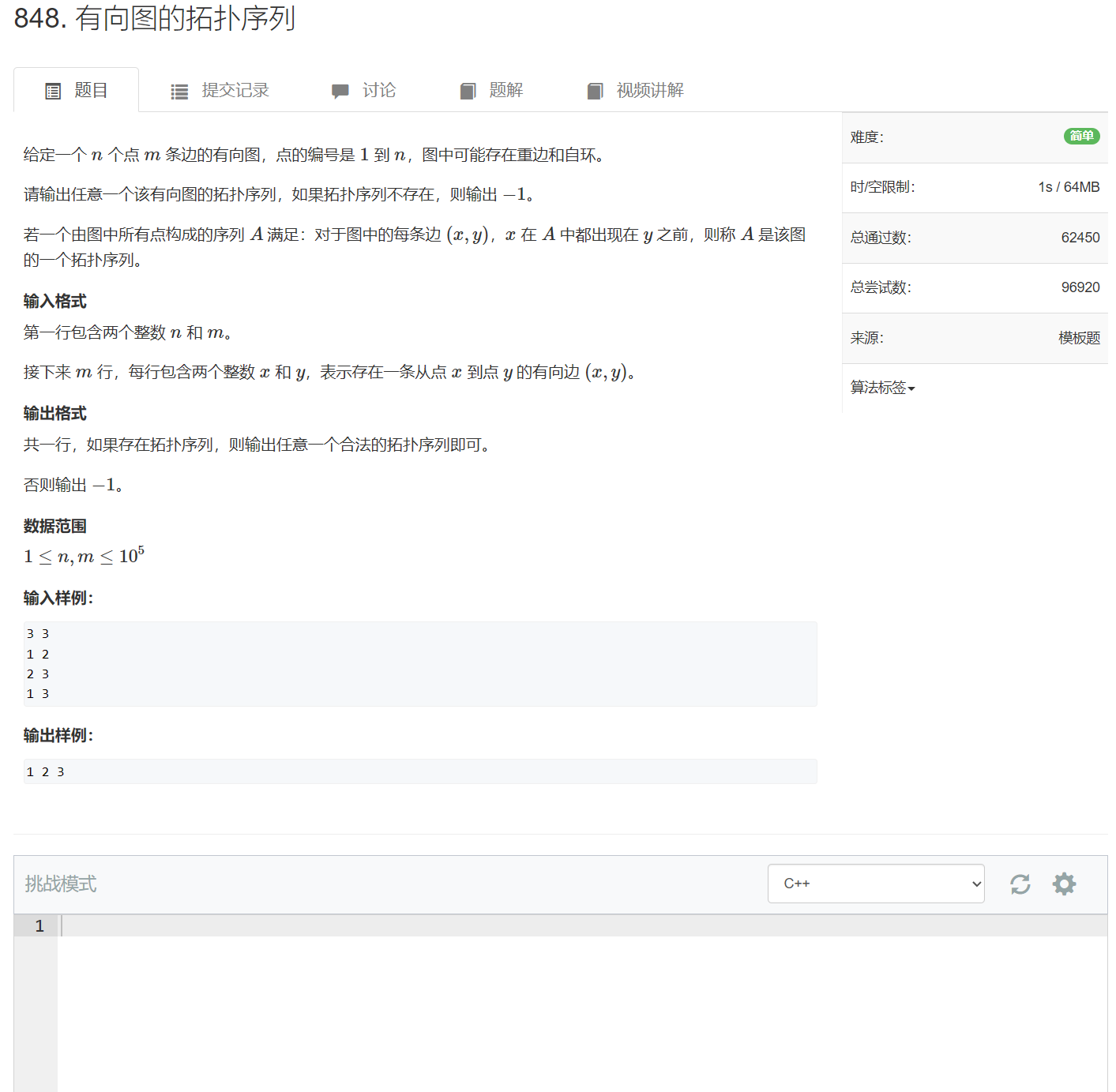
给定一个 n 个点 m 条边的有向图，点的编号是 1 到 n，图中可能存在重边和自环。

若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列。

拓扑排序过程

1. 将所有入度为0的点入队

2. 取出队头节点，输出该点并删去该点，同时将与其相连的边删去，且将与其相连的点的入度减去 1

3. 重复此过程，直到所有的点都输出完成

首先我们要明确一个有向无环图必定存在至少一个入度为0的点，所以以此为突破口，进行拓扑排序。

参考例题

链接：[有向图的拓扑排序](848. 有向图的拓扑序列 - AcWing题库)

代码实现

题外话：之前一遇到要用邻接表的题就畏惧了，从来没好好理解过，今天终于能体会到一丝感悟，拓扑排序是个开始！

#include<bits/stdc++.h>

using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)

const int N = 100010;
int e[N], ne[N], h[N], idx;  //邻接表相关

int d[N];   //存序号i的入度
int q[N];  //队列

int n,m;

void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

bool topsort(){
    int hh = 0, tt = -1;

    //将所有入度为0的点入队
    for(int i = 1; i <= n;i++){
        if(!d[i]) q[++tt] = i;
    }

    while(hh <= tt){
        auto t = q[hh++];  //取队头:这里可以看出出队时的顺序就是拓扑排序的顺序，且hh只是++，不是覆盖,所以最终直接输出n个元素即可得到拓扑序列

        //遍历与t相连的边:判断入度以及删边
        for(int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];

            d[j]--;  
            if(!d[j]) q[++tt] = j;   //入度为0入队
        }
    }

    return tt == n-1;   //若最终恰好输出了n个元素，则说明是拓扑序列
}

int main(){
    IOS;

    cin>>n>>m;
    memset(h, -1, sizeof h);  //初始化头节点

    int a,b;
    for(int i = 0; i < m;i++){
        cin>>a>>b;
        add(a,b);   //加边a->b

        d[b]++;  //入度++
    }

    //判断是否为拓扑排序
    if(topsort()){
        //根据上述分析可知，队列的前n个元素即为拓扑序列
        for(int i = 0; i < n;i++){
            cout<<q[i]<<" ";
        }
        cout<<endl;
    }else cout<<-1<<endl;

    return 0;
}

力扣： 210课程表II

刚好拿来练习拓扑排序

要注意一下有向边的指向

[题目链接](210. 课程表 II - 力扣（LeetCode）)

题目如下:

代码如下：

class Solution {
public:
//拓扑排序  数组模拟邻接表
    const static int N = 4020;
    int h[N],e[N],ne[N],idx;
    int d[N];   //入度
    int q[N];  //队列

    //加边
    void add(int a,int b){
        e[idx] = b, ne[idx] = h[a]; h[a] = idx++;
    }
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        memset(h,-1,sizeof h);

        for(auto v : prerequisites){
            int a = v[0],b = v[1];    //注意是谁指向谁,应该是先修课为起点
            add(b,a);   //b->a
            d[a]++;   //a入度++
        }

        int hh = 0 ,tt = -1;

        for(int i = 0; i < numCourses;i++){     //所有0入度的点入队
            if(!d[i]) q[++tt] = i;
        }

        while(hh <= tt){
            auto t = q[hh++];    //取队头，且指针后移（说明队头弹出）

            //删去与当前队头相连的边
            for(int i = h[t]; i != -1; i = ne[i]){
                int j = e[i];
                d[j]--;      //相当于删边
                if(!d[j]) q[++tt] = j;   //将新增的0入度点入队
            }
        }

        //恰好输出n个元素，即为拓扑序列
        if(tt == numCourses-1) {
            return vector<int>(q, q+numCourses);  //使用数组初始化vector
        }else return vector<int>();   //不是则返回空数组
    }
};